DAY 13 試題

問題描述

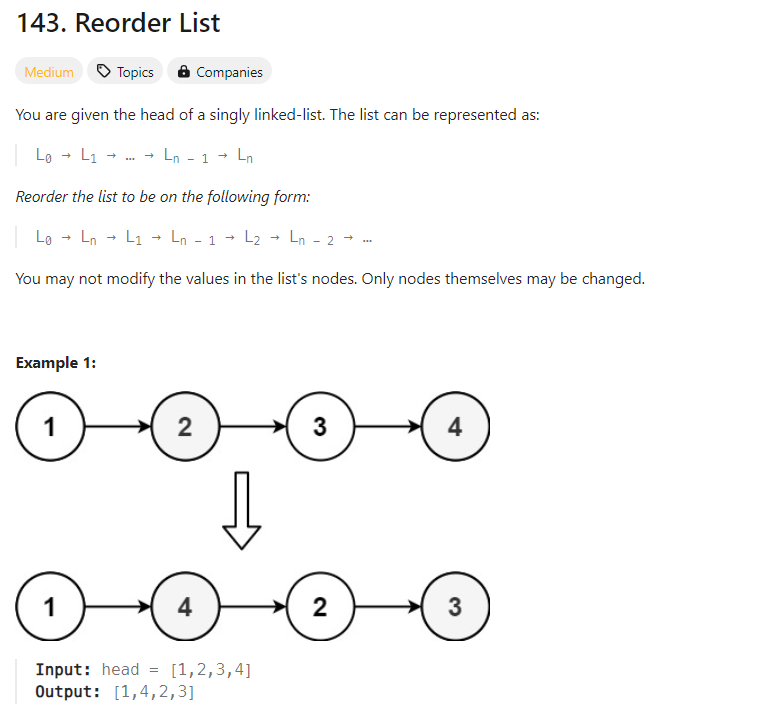
給定一個單鏈表的頭節點 head，該鏈表可以表示為：

L0 → L1 → L2 → … → Ln-1 → Ln

我們的目標是將鏈表重新排序，使其排列成：

L0 → Ln → L1 → Ln-1 → L2 → Ln-2 → …

注意：在此過程中，不允許修改節點中的值，只能變更節點之間的連接。

示例 1:

• 輸入: head = [1, 2, 3, 4]
• 輸出: [1, 4, 2, 3]

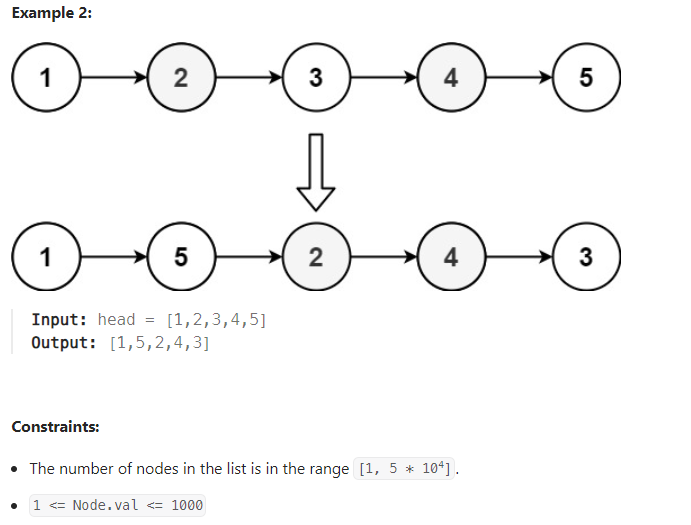
示例 2:

• 輸入: head = [1, 2, 3, 4, 5]
• 輸出: [1, 5, 2, 4, 3]

約束條件:

• 鏈表中的節點數量範圍是 [1, 5 * 10^4]。
• 每個節點的值範圍是 [1, 1000]。

解題思路

此題的思路是對鏈表的節點重新進行連接，而不能改變節點內的值。要達到這樣的效果，我們可以將此問題拆解為三個步驟：

1. 找到鏈表的中點： 使用快慢指針找到鏈表的中點。這是通過一個指針每次移動兩步，而另一個指針每次移動一步來實現的。當快指針到達鏈表末端時，慢指針剛好到達中點。

2. 反轉鏈表的後半部分： 找到中點後，將後半部分鏈表反轉。這樣後半部分的鏈表順序將變為 Ln → Ln-1 → …，以便與前半部分交替合併。

3. 合併兩部分鏈表： 最後，將前半部分與反轉後的後半部分進行交替合併。具體做法是，每次取一個前半部分的節點，接著取一個後半部分的節點，直到所有節點重新連接完畢。

// 定義單鏈表節點結構
struct ListNode {
    int val;
    ListNode* next;
    ListNode(int x) : val(x), next(nullptr) {}
};

class Solution {
public:
    void reorderList(ListNode* head) {
        if (!head || !head->next) return;

        // 步驟 1: 使用快慢指針找到中點
        ListNode* slow = head;
        ListNode* fast = head;
        while (fast->next && fast->next->next) {
            slow = slow->next;
            fast = fast->next->next;
        }

        // 步驟 2: 反轉後半部分鏈表
        ListNode* prev = nullptr;
        ListNode* curr = slow->next;
        slow->next = nullptr;  // 分離前半部分和後半部分
        while (curr) {
            ListNode* nextTemp = curr->next;
            curr->next = prev;
            prev = curr;
            curr = nextTemp;
        }

        // 步驟 3: 合併兩部分鏈表
        ListNode* first = head;
        ListNode* second = prev;  // 反轉後的後半部分
        while (second) {
            ListNode* temp1 = first->next;
            ListNode* temp2 = second->next;
            first->next = second;
            second->next = temp1;
            first = temp1;
            second = temp2;
        }
    }
};

解法重點與分析

1. 找到中點： 使用快慢指針的方式來找鏈表的中點。快指針每次移動兩步，慢指針每次移動一步。當快指針到達鏈表末端時，慢指針正好位於中點。這個方法的時間複雜度是 O(n)，其中 n 是鏈表的長度。

2. 反轉後半部分鏈表： 在找到中點後，我們反轉鏈表的後半部分。這可以通過使用三個指針的反轉技術來實現：prev、curr 和 next。反轉後，我們得到一個新的鏈表，其順序是 Ln → Ln-1 → …。這部分的時間複雜度也是 O(n)，因為我們需要遍歷鏈表的後半部分。

3. 合併兩部分鏈表： 合併時，我們從前半部分鏈表和反轉後的後半部分交替取出節點並連接起來。這一步同樣需要遍歷所有節點，時間複雜度為 O(n)。

4. 時間複雜度： 整個算法主要有三個步驟，分別是找到中點、反轉後半部分鏈表、以及合併兩部分鏈表。每個步驟都需要遍歷鏈表一次，所以時間複雜度是 O(n)。

5. 空間複雜度： 算法只使用了幾個指針變量來儲存中間結果，因此空間複雜度是 O(1)，這意味著我們沒有使用任何額外的空間來儲存鏈表節點的數據。

總結

這道題的核心是鏈表的重新連接，不能改變節點內的值。通過快慢指針尋找中點，反轉後半部分鏈表，再進行交替合併，我們可以在 O(n) 的時間複雜度內解決問題。這種方法充分利用了鏈表的特性，在不改變值的情況下，通過指針操作實現了所需的重排序。

以上是第十三天的自學內容分享，謝謝大家。